some vector analysis questions (a bit long)

[freeziepleasy]

Hello. I am studying vector analysis by myself in hopes to try my best as I can and to go as far as I can in mathematics so I can sit in a quantum mechanics class and understand what they are talking about. So, in short, this is not school work, since I'm studying by myself and not taking a class. The book I am using - "Vector Analysis" by L. Marder - is a very small, concise book, and he takes a lot of shortcuts in the mathematics he uses. I'm not a mathematics or physics major, so any questions I have about what he did will probably not be answered in his book, since it seems this book is very concentrated material.

1) Show that the unit vectors R hat, psi hat, z hat have cartesian components given by
R hat=(cosΨ,sinΨ,0)
Ψ hat=(-sinΨ,cosΨ,0)
z hat=(0,0,1)
and also that the curved surface of the cylinder in the Figure has the line element ds, where
ds^2=a^2dΨ^2 + dz^2,
and a is the radius.
If anyone needs the picture:


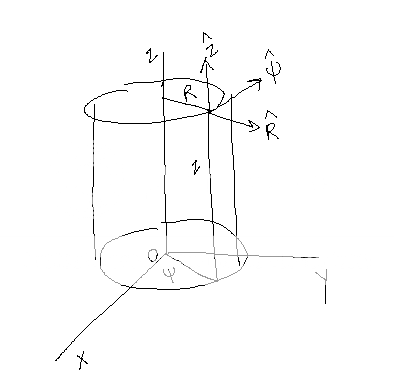
I got the cartesian components. I have a question about the line element.
For R, I have magnitude 1
for Ψ, magnitude is R
for z, magnitude is 1

When solving for line element, I ended up with
ds^2=(∂ r/∂ R)^2(dR)^2 + (∂ r/∂ Ψ)^2(dΨ)^2 + (∂r/∂z)^2(dz)^2 + ... (the other stuff that tends to zero because R, Ψ, and z are orthogonal to each other)
ds^2=1(dR)^2 + R^2(dΨ)^2 + (dz)^2

answer does not have dR^2 included. Why?

2) If you have cross product:
∂r/∂θ x ∂r/∂Ψ = a^2(sin^2θ cosΨi + sin^2θ sinΨj + sinθcosθk)

and so

|∂r/∂θ x ∂r/∂Ψ| = a^2(sin^4θ + sin^2θ cos^2θ)^(1/2) = a^2 sinθ

I got the answer for ∂r/∂θ x ∂r/∂Ψ, but not for the absolute value of it.
If I took the scalar of the vector:
sin^2θ cosΨi + sin^2θ sinΨj + sinθcosθk
I would end up with the answer for the absolute value.

Is that the correct way to get the answer? Why?
If it is not the correct way to get it, how else would you get it?
*He only stated the answer with no explanation.

3) For evaluation of flux through a surface,
I have trouble seeing how vector (∂f/∂x, ∂f/∂y, ∂f/∂z) is normal to the surface. How does a vector like this looks like?

4) If you have variables x and y, and you introduce polar coordinates R and Ψ into them, so that
x = RcosΨ
y = RsinΨ
then dxdy = RdRdΨ

Why is it RdRdΨ? Why can't it be dxdy = (dR)^2 (dΨ)^2?

5) Find flux of vector field F=zj-k through surface x=sinu cosv, y=sinu sinv , z=cos^2 u, where 0 ≦u ≦0.5pi, 0 ≦v < 2pi.

He did
dScos(n hat, k) = dSn hat . k = dxdy

doing this makes calculating flux automatically measured in the normal direction with k component.
I don't see how this is so. I also don't see why he did cos(n hat, k). And why when he takes

integral F.dS, he takes it by the value of S, but when he does double integral, he does it on So (s knot?), where So is a particular point on the surface (??)...
Is it just that integrating one time to the value of S is just standard to write it that way, but when you really solve for it with double integral, the So gives the parameters of the integral? So it's just standard way of writing?

I also have trouble picturing how vectors like
(∂f/∂x, ∂f/∂y, ∂f/∂z) look like on a graph
or
df = (∂f/∂xdx + ∂f/∂ydy + ∂f/∂zdz) look like on a graph. Are we supposed to remember that
(∂f/∂x, ∂f/∂y, ∂f/∂z) is always normal to surface
and
df = (∂f/∂xdx + ∂f/∂ydy + ∂f/∂zdz) is always tangential to surface at some point?
Or do I have this wrong?

Any answer to any of the questions would be appreciated. I know it's a long list of questions.

Thank you to anyone who helps.  

[VorpalNeko]

freeziepleasy

When solving for line element, I ended up with
ds^2=(∂ r/∂ R)^2(dR)^2 + (∂ r/∂ Ψ)^2(dΨ)^2 + (∂r/∂z)^2(dz)^2 + ... (the other stuff that tends to zero because R, Ψ, and z are orthogonal to each other)
ds^2=1(dR)^2 + R^2(dΨ)^2 + (dz)^2
answer does not have dR^2 included. Why?

I'm not sure what you're doing here, but it's true that in cylindrical coordinates (R,Ψ,z), the Euclidean metric takes the form ds² = dR² + R²dΨ² + dz², just as you have it, but the question was about a surface of constant R. Obviously, dR = 0 on that surface, say R = a.

Substitution's all well and good, but perhaps you're missing something important. The metric by definition finds inner products of tangent vectors, and you know from the first part the tangent vectors Ψ (= RΨ^, not normalized) and z corresponding to the surface. Thus, with those two as the basis,
g11 = Ψ·Ψ = R²; g12 = Ψ·z = 0 = g21; g22 = z·z = 1.
Therefore, you can simply read off the metric components from the usual
ds² = g11 dΨ² + g12 dΨdz + g21 dzdΨ + g22 dz²,
since all the relevant partial differentiation was already done in finding the orthonormal basis.

freeziepleasy

2) ...
Is that the correct way to get the answer? Why?

Yes, except for a factor of a², because the absolute value of a vector is just another name for the norm (|x| = sqrt(x·x)). I'm not sure what you're asking if you've already found the cross correctly.

freeziepleasy

3) For evaluation of flux through a surface,
I have trouble seeing how vector (∂f/∂x, ∂f/∂y, ∂f/∂z) is normal to the surface. How does a vector like this looks like?

I presume that you mean for a function f:R³→R, the surface is defined by f = c for some constant c, which would make the statement correct. One way to think of this is to continue interpreting the gradient as the proper generalization of derivative in higher dimensions (as we've done in the previous thread regarding integrals), so that what we really have is a chain-rule type of situation. To be more explicit, if you have think of a local patch of the surface as having the form (x,y,z) = F(u,v), then f(F(u,v)) = c differentiated gives ∇f·∂F/∂u = 0, but ∂F/∂u is just the surface tangent vector in the u-direction. Since the parametrization in terms of (u,v) is arbitrary, ∇f must orthogonal to every tangent vector of the surface.

Perhaps it'll be easier to visualize if you consider a curve γ on the surface that has constant coordinates y,z (i.e., only x is allowed to vary: γ = (X(t),Y,Z)). Then f(γ) = c differentiated is just makes use of the ordinary chain rule. Now consider what happens for a general curve where the y and z coordinates are allowed to vary--there are a now partials in those directions as well.

freeziepleasy

4) If you have variables x and y, and you introduce polar coordinates R and Ψ into them, so that
x = RcosΨ
y = RsinΨ
then dxdy = RdRdΨ

Why is it RdRdΨ? Why can't it be dxdy = (dR)^2 (dΨ)^2?

Simple answer: because that's what substitution gives you. Just differentiate: dx = dR cos Ψ - R sin Ψ dΨ, dy = ... and substitute in dx dy.
Deeper answer: because that's the volume element, which is the determinant of the metric tensor, and the determinant of the metric in those coordinates is RdRdΨ. Note: "volume" is a bit of a misnomer in the 2-dimensional case, since it's really area, but I'm using it in the general sense.
Intuitive answer: Start from some point with coordinates (R,Ψ) and plot (R,Ψ+dΨ), (R+dR,Ψ), and (R+dR,Ψ+dΨ). This is a curved region that's rectangular in the infinitesimal limit, with one side dR and another side along the circumference RdΨ. Hence the area element is RdRdΨ in polar coordinates. If you do the same thing in Cartesian coordinates, we would get dxdy. Since areas of regions are independent of which coordinates we use, they better be equal.

freeziepleasy

5) Find flux of vector field F=zj-k through surface x=sinu cosv, y=sinu sinv , z=cos^2 u, where 0 ≦u ≦0.5pi, 0 ≦v < 2pi.

The notation you've used there doesn't make much sense to me, so I'm not sure what you're doing here. However, that looks like a paraboloid of revolution: r²+z-1 = 0 in cylindrical coordinates. You're probably going to end up trying to make it into an integral over a region in the xy plane (dA = dxdy = rdrdΨ).

Or, you can probably just tie everything together and look at the induced metric over the surface: ds² = sin²u dv² + [5-4cos²u]cos²u du². Hence the surface area element is just the determinant of the metric, dS = [5-4cos²u]sin²u cos²u du dv, and you can get a surface normal with that cross product you were doing earlier, but this method is a lot messier. You should probably double-check that, though, because I'm too lazy to do so.

freeziepleasy

I also have trouble picturing how vectors like
(∂f/∂x, ∂f/∂y, ∂f/∂z) look like on a graph

It's in the direction of the greatest increase of f, with the magnitude being the slope in that direction. In general, ∇f·r is the ordinary derivative (slope) in the r direction.

freeziepleasy

or df = (∂f/∂xdx + ∂f/∂ydy + ∂f/∂zdz) look like on a graph.

I usually try to picture those differentials as pairs of infinitesimal planar regions. I can try to explain the picture later in more detail if you want, but right now I've done too much typing already.