PreliminariesBefore delving into relativity, let's first briefly review some concepts from coordinate geometry. Consider the standard (x,y) coordinate plane, which is governed by the Euclidean metric ds² = dx²+dy². This may look fancy to those without familiarity with calculus, but it is really just the Pythagorean theorem. The distance s between two points (x,y) and (a,b) is the length of the line segment between them, which can be thought of as the hypotenuse of a right triangle with sides |x-a| and |y-b|, leading to the familiar distance formula s² = (x-a)² + (y-b)², as per the Pythagorean theorem.
Exercise 1: [Geom] In three dimensions, show that the distance formula between two points (x,y,z) and (a,b,c) extends naturally to s² = (x-a)² + (y-b)² + (z-c)². In differential form, this is written as ds² = dx²+dy²+dz².
---
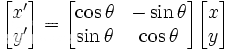
The locus of all points a certain distance r from the origin is simply the circle r² = x²+y²; in parametric form, this is {x = r cos t, y = r sin t}. Rotations through the origin leave this distance fixed, so that points stay on the same circle. If a point (x,y) is rotated counterclockwise by an angle θ, the new coordinates (x',y') are found by
x' = (cos θ)x - (sin θ)y
y' = (sin θ)x + (cos θ)y
Or, in matrix notation, [x';y'] = [cos θ, -sin θ; sin θ, cos θ ][x;y], where a semicolon indicates a new row (see image). Note that rotating every point counterclockwise is equivalent to rotating the coordinate axes themselves in the clockwise direction.
Exercise 2: [Trig] Prove that the above rotation formula works.
Rotations in three dimensions are combinations of three basic rotations: around the x-axis by α, which leaves the x-coordinate the same rotates only in the (y,z) plane; around the y-axis by β, which occurs in the (x,z) plane and leaves y invariant; and finally around the z-axis by γ, which occur in the (x,y) plane. Thus, we can simply "embed" the two-dimensional rotational matrix in a 3x3 that one leaves the corresponding coordinate invariant. In matrix form, rotation about the x-axis takes the form: R_x = [ 1, 0, 0; 0, cos α, -sin α; 0 sin α, cos α ]. All three-dimensional rotations can be decomposed into a sequence of these basic rotations.
Exercise 3: [Matr] Find the three-dimensional rotation matrices R_y and R_z.
---
A complex number is defined as a pair of real numbers (x,y), subject to the the following rules of arithmetic:
(x,y)+(a,b) = (x+a,y+b)
(x,y)·(a,b) = (xa-yb,xb+ya)
Complex numbers are commutative (w·z = z·w, w+z = z+w), associative ((w·z)·c = w·(z·c), (w+z)+c = w+(z+c)), and distributive (w·(z+c) = w·z+w·c)), where w = (u,v), z = (x,y) and c = (a,b) are arbitrary complex numbers. Complex numbers can be interpreted as points in the "complex plane"--the pair of numbers (x,y) being the standard Cartesian coordinates.
Exercise 4: [Alg] Assuming the corresponding properties of real numbers (commutativity, associativity, distributivity), verify that complex numbers satisfy them also.
Defining i = (0,1) and identifying every real number x with the complex number (x,0), a complex number z = (x,y) can be written simply as z = (x,y) = (x,0) + (0,1)·(y,0) = x+iy. Since i² = (-1,0) = -1, this form allows for easy computations with complex numbers. For example, (3+2i)+(-1+4i) = 2+6i, while (3+2i)·(-1+4i) = -3+12i-2i+8i² = -11+10i.
[work in progress]
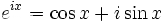
The final tool in our arsenal is complex exponentiation, Euler's formula to be precise: e^{it} = exp(it) = cos t + i sin t. This is a very powerful tool that can be used to prove numerous trigonometric identities. For example, cos(s+t) + i sin(s+t) = e^{is+it} = e^{is}e^{it} = (cos s + i sin t)(cos s + i sin t). Multiplying this out and setting the respective real and imaginary components equal to each other, we have cos(s+t) = cos s cos t - sin s sin t and sin(s+t) = cos s sin t + sin s cos t, which are the familiar angle addition identities.
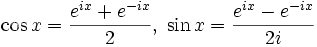
Exercise 5: [Alg] Show that cos t = [e^{it} + e^{-it}]/2 and sin t = [e^{it}-e^{-it}]/2i.
Following the above form, the hyperbolic trigonometric functions are defined as cosh t = [e^t + e^{-t}]/2 and sinh t = [e^t - e^{-t}]/2. Analogously to cos²t + sin²t = 1, we have cosh²t - sinh²t = 1.
Exercise 6: [Alg] Show that cos(it) = cosh(t), sin(it) = i sinh(t). Conclude that cosh²t - sinh²t = 1.
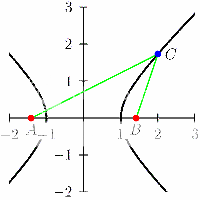
Just as the parametric equations {x = a cos t, y = b sin t} describe an ellipse, the equations {x = a cosh t, y = sinh t} describe a hyperbola, or rather, one branch of a hyperbola. The other branch is {x = -a cosh t, y = b sinh t}.
Exercise 7: [Alg] Let A be the point (-sqrt(2),0) and B be the point (sqrt(2),0). Show if C is the point (cosh t, sinh t), t any real number, then AC - BC = 2. Conclude that all points (cosh t, sinh t) lie on the same hyperbola with foci A and B.


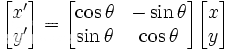 The locus of all points a certain distance r from the origin is simply the circle r² = x²+y²; in parametric form, this is {x = r cos t, y = r sin t}. Rotations through the origin leave this distance fixed, so that points stay on the same circle. If a point (x,y) is rotated counterclockwise by an angle θ, the new coordinates (x',y') are found by
The locus of all points a certain distance r from the origin is simply the circle r² = x²+y²; in parametric form, this is {x = r cos t, y = r sin t}. Rotations through the origin leave this distance fixed, so that points stay on the same circle. If a point (x,y) is rotated counterclockwise by an angle θ, the new coordinates (x',y') are found by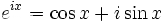 The final tool in our arsenal is complex exponentiation, Euler's formula to be precise: e^{it} = exp(it) = cos t + i sin t. This is a very powerful tool that can be used to prove numerous trigonometric identities. For example, cos(s+t) + i sin(s+t) = e^{is+it} = e^{is}e^{it} = (cos s + i sin t)(cos s + i sin t). Multiplying this out and setting the respective real and imaginary components equal to each other, we have cos(s+t) = cos s cos t - sin s sin t and sin(s+t) = cos s sin t + sin s cos t, which are the familiar angle addition identities.
The final tool in our arsenal is complex exponentiation, Euler's formula to be precise: e^{it} = exp(it) = cos t + i sin t. This is a very powerful tool that can be used to prove numerous trigonometric identities. For example, cos(s+t) + i sin(s+t) = e^{is+it} = e^{is}e^{it} = (cos s + i sin t)(cos s + i sin t). Multiplying this out and setting the respective real and imaginary components equal to each other, we have cos(s+t) = cos s cos t - sin s sin t and sin(s+t) = cos s sin t + sin s cos t, which are the familiar angle addition identities.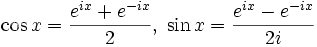 Exercise 5: [Alg] Show that cos t = [e^{it} + e^{-it}]/2 and sin t = [e^{it}-e^{-it}]/2i.
Exercise 5: [Alg] Show that cos t = [e^{it} + e^{-it}]/2 and sin t = [e^{it}-e^{-it}]/2i.  Just as the parametric equations {x = a cos t, y = b sin t} describe an ellipse, the equations {x = a cosh t, y = sinh t} describe a hyperbola, or rather, one branch of a hyperbola. The other branch is {x = -a cosh t, y = b sinh t}.
Just as the parametric equations {x = a cos t, y = b sin t} describe an ellipse, the equations {x = a cosh t, y = sinh t} describe a hyperbola, or rather, one branch of a hyperbola. The other branch is {x = -a cosh t, y = b sinh t}.